Sıkıştırma algoritmaları temel olarak iki kategoride incelenir. Bunlar, kayıplı ve kayıpsız sıkıştırma algoritmalarıdır. Kayıplı algoritmalarda sıkıştırılan veriden orjinal veri elde edilemezken kayıpsız sıkıştırma algoritmalarında sıkıştırılmış veriden orjinal veri elde edilebilir. Kayıplı sıkıştırma tekniklerine verilebilecek en güzel örnekler MPEG ve JPEG gibi standartlarda kullanılan sıkıştırmalardır. Bu tekniklerde sıkıştırma oranı artırıldığında orjinal veride bozulmalar ve kayıplar görülür. Örneğin sıkıştırılmış resim formatı olan JPEG dosyalarının kaliteli yada az kaliteli olmasının nedeni sıkıştırma katsayısıdır. Yani benzer iki resim dosyasından daha az disk alanı kaplayan daha kötü kalitededir deriz. Kayıpsız veri sıkıştırmada durum çok farklıdır. Bu tekniklerde önemli olan orjinal verilerin aynen sıkıştırılmış veriden elde edilmesidir. Bu teknikler daha çok metin tabanlı verilen sıkıştırılmasında kullanılır. Bir metin dosyasını sıkıştırdıktan sonra metindeki bazı cümlelerin kaybolması istenmediği için metin sıkıştırmada bu yöntemler kullanılır.
Bu yazının konusu olan Huffman sıkıştırma algoritması kayıpsız bir veri sıkıştırma tekniğini içerir. Bu yüzden bu yöntemin en elverişli olduğu veriler metin tabanlı verilerdir. Bu yazıda verilecek örnek programdaki hedef metin tabanlı verilerin sıkıştırılması olacaktır.
Huffman algoritması, bir veri kümesinde daha çok rastlanan sembolü daha düşük uzunluktaki kodla, daha az rastlanan sembolleri daha yüksek uzunluktaki kodlarla temsil etme mantığı üzerine kurulmuştur. Bir örnekten yola çıkacak olursak : Bilgisayar sistemlerinde her bir karakter 1 byte yani 8 bit uzunluğunda yer kaplar. Yani 10 karakterden oluşan bir dosya 10 byte büyüklüğündedir. Çünkü her bir karakter 1 byte büyüklüğündedir. Örneğimizdeki 10 karakterlik veri kümesi "aaaaaaaccs" olsun. "a" karakteri çok fazla sayıda olmasına rağmen "s" karakteri tektir. Eğer bütün karakterleri 8 bit değilde veri kümesindeki sıklıklarına göre kodlarsak veriyi sembolize etmek için gereken bitlerin sayısı daha az olacaktır. Söz gelimi "a" karakteri için "0" kodunu "s" karakteri için "10" kodunu, "c" karakteri için "11" kodunu kullanabiliriz. Bu durumda 10 karakterlik verimizi temsil etmek için
(a kodundaki bit sayısı)*(verideki a sayısı) + (c kodundaki bit sayısı)*(verideki c sayısı) + (s kodundaki bit sayısı)*(verideki s sayısı) = 1*7 + 2*2 + 2*1 = 12 bit
gerekecektir. Halbuki bütün karakterleri 8 bit ile temsil etseydik 8*10 = 80 bite ihtiyacımız olacaktı. Dolayısıyla %80 ’in üzerinde bir sıkıştırma oranı elde etmiş olduk. Burada dikkat edilmesi gereken nokta şudur : Veri kümesindeki sembol sayısına ve sembollerin tekrarlanma sıklıklarına bağlı olarak Huffman sıkıştırma algoritması %10 ile %90 arasında bir sıkıştırma oranı sağlayabilir. Örneğin içinde 2000 tane "a" karakteri ve 10 tane "e" karakteri olan bir veri kümesi Huffman tekniği ile sıkıştırılırsa %90’lara varan bir sıkıştırma oranı elde edilir.
Huffman tekniğinde semboller(karakterler) ASCII’de olduğu gibi sabit uzunluktaki kodlarla kodlanmazlar. Her bir sembol değişken sayıda uzunluktaki kod ile kodlanır.
Bir veri kümesini Huffman tekniği ile sıkıştırabilmek için veri kümesinde bulunan her bir sembolün ne sıklıkta tekrarlandığını bilmemiz gerekir. Örneğin bir metin dosyasını sıkıştırıyorsak her bir karakterin metin içerisinde kaç adet geçtiğini bilmemiz gerekiyor. Her bir sembolün ne sıklıkta tekrarlandığını gösteren tablo frekans tablosu olarak adlandırılmaktadır. Dolayısıyla sıkıştırma işlemine geçmeden önce frekans tablosunu çıkarmamız gerekmektedir. Bu yönteme Statik Huffman tekniği de denilmektedir. Diğer bir teknik olan Dinamik Huffman tekniğinde sıkıştırma yapmak için frekans tablosuna önceden ihtiyaç duyulmaz. Frekans tablosu her bir sembolle karşılaştıkça dinamik olarak oluşturulur. Dinamik Huffman tekniği daha çok haberleşme kanalları gibi hangi verinin geleceği önceden belli olmayan sistemlerde kullanılmaktadır. Bilgisayar sistemlerindeki dosyaları sıkıştırmak için statik huffman metodu yeterlidir. Nitekim bir dosyayı baştan sona tarayarak herbir sembolün hangi sıklıkla yer aldığını tespit edip frekans tablosunu elde etmemiz çok basit bir işlemdir.
Huffman sıkıştırma tekniğinde frekans tablosunu elde etmek için statik ve dinamik yaklaşımlarının olduğunu söyledik. Eğer statik yöntem seçilmişse iki yaklaşım daha vardır. Birinci yaklaşım, metin dosyasının diline göre sabit bir frekans tablosunu kullanmaktır. Örneğin Türkçe bir metin dosyasında "a" ve "e" harflerine çok sık rastlanırken "ğ" harfine çok az rastlanır. Dolayısıyla "ğ" harfi daha fazla bitle "a" ve "e" harfi daha az bitle kodlanır. Frekans tablosunu elde etmek için kullanılan diğer bir yötem ise metni baştan sona tarayarak her bir karakterin frekansını bulmaktır. Sizde takdir edersinizki ikinci yöntem daha gerçekçi bir çözüm üretmekle beraber metin dosyasının dilinden bağımsız bir çözüm üretmesi ile de ön plandadır. Bu yöntemin dezavantajı ise sıkıştırılan verilerde geçen sembollerin frekansının da bir şekilde saklanma zorunluluğunun olmasıdır. Sıkıştırılan dosyada her bir sembolün frekansıda saklanmalıdır. Bu da küçük boyutlu dosyalarda sıkıştırma yerine genişletme etkisi yaratabilir. Ancak bu durum Huffman yönteminin kullanılabililiğini zedelemez. Nitekim küçük boyutlu dosyaların sıkıştırılmaya pek fazla ihtiyacı yoktur zaten.
Frekans tablosunu metin dosyasını kullanarak elde ettikten sonra yapmamız gereken "Huffman Ağacını" oluşturmaktır. Huffman ağacı hangi karakterin hangi bitlerle temsil edileceğini(kodlanacağını) belirlememize yarar. Birazdan örnek bir metin üzerinden "Huffman Ağacını" teorik olarak oluşturup algoritmanın derinliklerine ineceğiz. Bu örneği iyi bir şekilde incelediğinizde Huffman algoritmasının aslında çok basit bir temel üzerine kurulduğunu göreceksiniz.
Huffman Ağacının Oluşturulması
Bir huffman ağacı aşağıdaki adımlar izlenerek oluşturulabilir.
Bu örnekte aşağıdaki frekans tablosu kullanılacaktır.

u tablodan çıkarmamız gereken şudur : Elimizde öyle bir metin dosyası varki "a" karakteri 50 defa, "b" karakteri 35 defa .... "ğ" karakteri 2 defa geçiyor. Amacımız ise her bir karakteri hangi bit dizileriyle kodlayacağımızı bulmak.
1 - Öncelikle "Huffman Ağacını" ndaki en son düğümleri(dal) oluşturacak bütün semboller frekanslarına göre aşağıdaki gibi küçükten büyüğe doğru sıralanırlar.

2 - En küçük frekansa sahip olan iki sembolün frekansları toplanarak yeni bir düğüm oluşturulur. Ve oluşturulan bu yeni düğüm diğer varolan düğümler arasında uygun yere yerleştirilir. Bu yerleştirme frekans bakımından küçüklük ve büyüklüğe göredir. Örneğin yukarıdaki şekilde "ğ" ve "d" sembolleri toplanarak "12" frakansında yeni bir "ğd" düğümü elde edilir. "12" frekanslı bir sembol şekilde "m" ve "k" sembolleri arasında yerleştirilir. "ğ" ve "d" düğümleri ise yeni oluşturulan düğümün dalları şeklinde kalır. Yeni dizimiz aşağıdaki şekilde olacaktır.
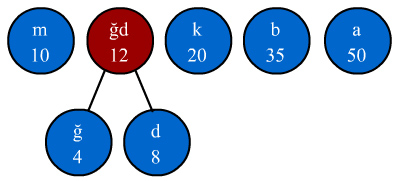
3 - 2.adımdaki işlem tekrarlanarak en küçük frekanslı iki düğüm tekrar toplanır ve yeni bir düğüm oluşturulur. Bu yeni düğümün frekansı 22 olacağı için "k" ve "b" düğümleri arasına yerleşecektir. Yeni dizimiz aşağıdaki şekilde olacaktır.
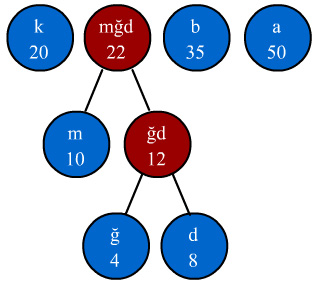
4 - 2.adımdaki işlem tekrarlanarak en küçük frekanslı iki düğüm tekrar toplanır ve yeni bir düğüm oluşturulur. Bu yeni düğümün frekansı 42 olacağı için "b" ve "a" düğümleri arasına yerleşecektir. Yeni dizimiz aşağıdaki şekilde olacaktır. Dikkat ederseniz her dalın en ucunda sembollerimiz bulunmaktadır. Dalların ucundaki düğümlere özel olarak yaprak(leaf) denilmektedir. Sona yaklaştıkça Bilgisayar bilimlerinde önemli bir veri yapısı olan Tree(ağaç) veri yapısına yaklaştığımızı görüyoruz.
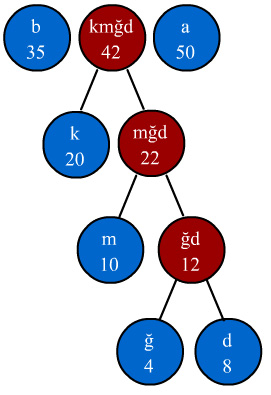
5 - 2.adımdaki işlem tekrarlanarak en küçük frekanslı iki düğüm tekrar toplanır ve yeni bir düğüm oluşturulur. Bu yeni düğümün frekansı 77 olacağı için "a" düğümünden sonra yerleşecektir. Yeni dizimiz aşağıdaki şekilde olacaktır. Dikkat ederseniz her bir düğümün frekansı o düğümün sağ ve sol düğümlerinin frekanslarının toplamına eşit olmaktadır. Aynı durum düğüm sembolleri içinde geçerlidir.
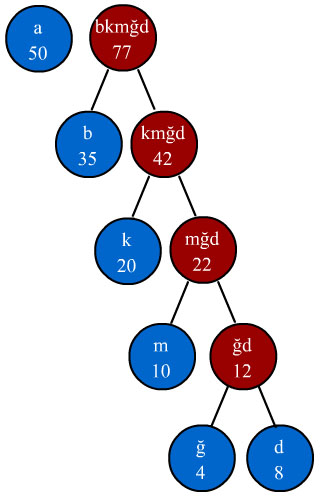
6 - 2.adımdaki işlem en tepede tek bir düğüm kalana kadar tekrar edilir. En son kalan düğüm Huffman ağacının kök düğümü(root node) olarak adlandırılır. Son düğümün frekansı 127 olacaktır. Böylece huffman ağacının son hali aşağıdaki gibi olacaktır.
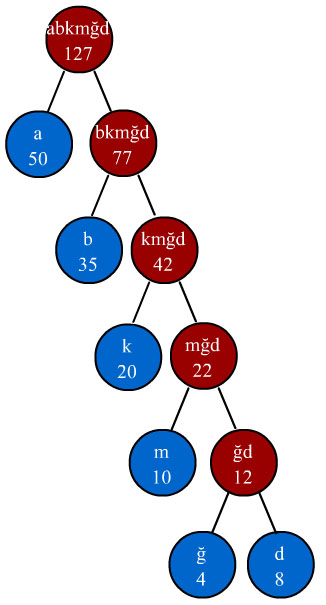
Not : Dikkat ederseniz Huffman ağacının son hali simetrik bir yapıda çıktı. Yani yaprak düğümler hep sol tarafta çıktı. Bu tamamen seçtiğimiz sembol frekanslarına bağlı olarak rastlantısal bir sonuçtur. Bu rastlantının oluşması oluşturduğumuz her bir yeni düğümün yeni dizide ikinci sıraya yerleşmesinden kaynaklanmaktadır. Sembol frekanslarında değişiklik yaparak ağacın şeklindeki değişiklikleri kendinizde görebilirsiniz.
7 - Huffman ağacının son halini oluşturduğumuza göre her bir sembolün yeni kodunu oluşturmaya geçebiliriz. Sembol kodlarını oluşturuken Huffman ağacının en tepesindeki kök düğümden başlanır. Kök düğümün sağ ve sol düğümlerine giden dala sırasıyla "0" ve "1" kodları verilir. Sırası ters yönde de olabilir. Bu tamamen seçime bağlıdır. Ancak ilk seçtiğiniz sırayı bir sonraki seçimlerde korumanız gerekmektedir. Bu durumda "a" düğümüne gelen dal "0", "bkmğd" düğümüne gelen dal "1" olarak seçilir. Bu işlem ağaçtaki tüm dallar için yapılır. Dalların kodlarla işaretlenmiş hali aşağıdaki gibi olacaktır.
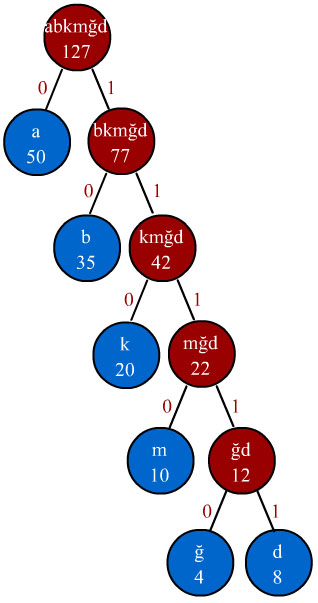
8 - Sıra geldi her bir sembolün hangi bit dizisiyle kodlanacağını bulmaya. Her bir sembol dalların ucunda bulunduğu için ilgili yaprağa gelene kadar dallardaki kodlar birleştirilip sembollerin kodları oluşturulur. Örneğin "a" karakterine gelene kadar yalnızca "0" dizisi ile karşılaşırız. "b" karakterine gelene kadar önce "1" dizisine sonra "0" dizisi ile karşılaşırız. Dolayısıyla "b" karakterinin yeni kodu "10" olacaktır. Bu şekilde bütün karakterlerin sembol kodları çıkarılır. Karakterlerin sembol kodları aşağıda bir tablo halinde gösterilmiştir.

Sıkıştırılmış veride artık ASCII kodları yerine Huffman kodları kullanılacaktır. Dikkat ederseniz hiçbir Huffman kodu bir diğer Huffman kodunun ön eki durumunda değildir. Örneğin ön eki "110" olan hiç bir Huffman kodu mevcut değildir. Aynı şekilde ön eki "0" olan hiç bir Huffman kodu yoktur. Bu Huffman kodları ile kodlanmış herhangi bir veri dizisinin "tek çözülebilir bir kod" olduğunu göstermektedir. Yani sıkıştırılmış veriden orjinal verinin dışında başka bir veri elde etme ihtimali sıfırdır. (Tabi kodlamanın doğru yapıldığını varsayıyoruz.)
Şimdi örneğimizdeki gibi bir frekans tablosuna sahip olan metnin Huffman algoritması ile ne oranda sıkışacağını bulalım :
Sıkıştırma öncesi gereken bit sayısını bulacak olursak : Her bir karakter eşit uzunlukta yani 8 bit ile temsil edildiğinden toplam karakter sayısı olan (50+35+20+10+8+4) = 127 ile 8 sayısını çarpmamız lazım. Orjinal veriyi sıkıştırmadan saklarsak 127*8 = 1016 bit gerekmektedir.
Huffman algoritmasını kullanarak sıkıştırma yaparsak kaç bitlik bilgiye ihtiyaç duyacağımızı hesaplayalım : 50 adet "a" karakteri için 50 bit, 35 adet "b" karakteri için 70 bit, 20 adet "k" karakteri için 60 bit....4 adet "ğ" karakteri için 20 bite ihtiyaç duyarız. (yukarıdaki tabloya bakınız.) Sonuç olarak gereken toplam bit sayısı = 50*1 + 35*2 + 20*3 + 10*4 + 8*5 + 4*5 = 50 + 70 + 60 + 40 + 40 + 20 = 280 bit olacaktır.
Sonuç : 1016 bitlik ihtiyacımızı 280 bite indirdik. Yani yaklaşık olarak %72 gibi bir sıkıştırma gerçekleştirmiş olduk. Gerçek bir sistemde sembol frekanslarınıda saklamak gerektiği için sıkıştırma oranı %72’ten biraz daha az olacaktır. Bu fark genelde sıkıştırılan veriye göre çok çok küçük olduğu için ihmal edilebilir.
Huffman Kodunun Çözülmesi
Örnekte verilen frekans tablosuna sahip bir metin içerisindeki "aabkdğmma" veri kümesinin sıkıştırılmış hali her karakter ile karakterin kodu yer değiştirilerek aşağıdaki gibi elde edilir.
a a b k d ğ m m a
0 0 10 110 11111 11110 1110 1110 0 --> 00101101111111110111011100
Eğer elimizde frekans tablosu ve sıkıştırılmış veri dizisi varsa işlemlerin tersini yaparak orjinal veriyi elde edebiliriz. Şöyleki; sıkıştırılmış verinin ilk biti alnır. Eğer alınan bit bir kod sözcüğüne denk geliyorsa, ilgili kod sözcüğüne denk düşen karakter yerine koyulur, eğer alınan bit bir kod sözcüğü değilse sonraki bit ile birlikte ele alınır ve yeni dizinin bir kod sözcüğü olup olmadığına bakılır. Bu işlem dizinin sonuna kadar yapılır ve huffman kodu çözülür. Huffman kodları tek çözülebilir kod olduğu için bir kod dizisinden farklı semboller elde etmek olanaksızdır. Yani bir huffman kodu ancak ve ancak bir şekilde çözülebilir. Bu da aslında yazının başında belirtilen kayıpsız sıkıştırmanın bir sonucudur.
C# ile Huffman Algoritmasının Gerçekleştirilmesi
Huffman algoritması bilgisayar bilimlerinde genellikle metin dosyalarının sıkıştırılmasında kullanılır. Bu yazıda örnek bir program ile Huffman algoritmasının ne şekilde uygulanacabileceğini de göreceğiz. Dil olarak tabiki C#’ı kullanılacaktır.
Huffman algoritmasının uygulanmasındaki ilk adım frekans tablosunun bulunmasıdır. Bu yüzden bir dosyayı sıkıştırmadan önce dosyadaki her bir karakterin ne sıklıkla yer aldığını bulmak gerekir. Örnek programda sembol frekanslarını bellekte tutmak için System.Collections isim alanıdan bulunan Hashtable koleksiyon yapısı kullanılmıştır. Örneğin "c" karakterinin frekansı 47 ise,
CharFrequencies["c"] = 47
şeklinde sembolize edilir. Örnek programda frekans tablosu aşağıdaki metot ile elde edilebilir. Sıkıştırılacak dosya baştan sona taranarak frekanslar hashtable nesnesine yerleştirilir.
[Not : Örnek uygulamada kullandığım değişken ve metot isimlerini bazı özel nedenlerden dolayı İngilizce yazmak zorunda kaldığım için tüm okurlardan özür dilerim.]
private Hashtable CharFrequencies = new Hashtable();
private void MakeCharFrequencies()
{
FileStream fs = File.Open(file,FileMode.Open,FileAccess.Read); StreamReader sr = new StreamReader(fs,System.Text.Encoding.ASCII);
int iChar;
char ch;
while((iChar = sr.Read()) != -1)
{
ch = (char)iChar;
if(!CharFrequencies.ContainsKey(ch.ToString()))
{
CharFrequencies.Add(ch.ToString(),1);
}
else
{
int oldFreq = (int)CharFrequencies[ch.ToString()];
int newFreq;
newFreq = oldFreq + 1;
CharFrequencies[ch.ToString()] = newFreq;
}
}
sr.Close();
fs.Close();
sr = null;
fs = null;
}
Frekans tablosunu yukarıdaki metot yardımıyla oluşturduktan sonra huffman algoritmasının en önemli adımı olan huffman ağacının oluşturulmasına sıra geldi. Huffman ağacının oluşturulması en önemli ve en kritik noktadır. Huffman ağacı oluşturulurken Tree(ağaç) veri yapısından faydalanılmıştır. Ağaçtaki her bir düğümü temsil etmek için bir sınıf yazılmıştır. Huffman ağacındaki düğümleri temsil etmek için kullanılabilecek en basit düğüm sınıfının yapısı aşağıdaki gibidir.

Yukarıdaki düğüm yapısı algoritmayı uygulamak için gereken en temel düğüm yapısıdır. Bu yapı istenildiği gibi genişletilebilir. Önemli olan minimum gerekliliği sağlamaktır. Düğüm sınıfındaki SagDüğüm ve SolDüğüm özellikleri de düğüm türündendir. Başlangıçtaki düğümler için bu değerler null dır. Her bir yeni düğümm oluşturulduğunda yeni düğümün sağ ve sol düğümleri oluşur. Ancak unutmamak gerekir ki sadece sembollerimizi oluşturan yaprak düğümlerde bu özellikler null değerdedir.
Örnek uygulamadaki HuffmanNode sınıfında ayrıca ilgili düğümün yaprak olup olmadığını gösteren IsLeaf ve ilgili düğümün ana(parent) düğümünü gösteren HuffmanNode türünden ParentNode özellikleri bulunmaktadır.
HuffmanNode düğüm sınıfının yapısı aşağıdaki gibidir.
using System; namespace Huffman
{
public class HuffmanNode
{
private HuffmanNode leftNode;
private HuffmanNode rightNode;
private HuffmanNode parentNode;
private string symbol;
private int frequency;
private string code = "";
private bool isLeaf;
public HuffmanNode LeftNode
{
get{return leftNode;}
set{leftNode = value;}
}
public HuffmanNode RightNode
{
get{return rightNode;}
set{rightNode = value;}
}
public HuffmanNode ParentNode
{
get{return parentNode;}
set{parentNode = value;}
}
public string Symbol
{
get{return symbol;}
set{symbol = value;}
}
public string Code
{
get{return code;}
set{code = value;}
}
public int Frequency
{
get{return frequency;}
set{frequency = value;}
}
public bool IsLeaf
{
get{return isLeaf;}
set{isLeaf = value;}
}
public HuffmanNode()
{
}
}
public class NodeComparer : IComparer
{
public NodeComparer()
{
}
public int Compare(object x, object y)
{
HuffmanNode node1 = (HuffmanNode)x;
HuffmanNode node2 = (HuffmanNode)y;
return node1.Frequency.CompareTo(node2.Frequency);
}
}
}
Başlangıçta sembol sayısı kadar HuffmanNode nesnesi yani huffman düğümü oluşturmamız gerekecektir. Oluşturulan bu düğümler Arraylist koleksiyon yapısında tutulmaktadır. Her bir yeni düğüm oluşturulduğunda Arraylist kolaksiyonun yeni bir düğüm eklenir ve iki düğüm çıkarılır. Yeni düğümün sağ ve sol düğümleri çıkarılan düğümler olacaktır. İlk oluşturulan düğümlerin sağ ve sol düğümlerinin null olduğunu hatırlayınız. Yeni düğüm eklendiğinde Arraylist sınıfının Sort() metodu yardımıyla düğümler frekanslarına göre küçükten büyüğe doğru sıralanır. Yani Arraylist elemanını ilk elemanı en küçük frekanslı düğümdür. Sort() metodu IComparer arayüzünü kullanan NodeComparer sınıfını kullanmaktadır. Yani bu sınıftaki Compare() metodu yukarıdaki kodda belirtildiği gibi düğüm nesnelerinin neye göre sıralancağını tanımlar.
Yukarıdaki tanımlar ışığında Huffman ağacı aşağıdaki metot yardımıyla bulunabilir. Dikkat ettiyseniz, metodun icrası bittiğinde Nodes koleksiyonunda tek bir düğüm nesnesi kalacaktır, bu da huffman ağacındaki kök düğümden(root node) başkası değildir.
private ArrayList Nodes;
public void MakeHuffmanTree()
{
Nodes = new ArrayList(); //Başlangıç düğümleri oluşturuluyor.
foreach(Object Key in CharFrequencies.Keys)
{
HuffmanNode node = new HuffmanNode();
node.LeftNode = null;
node.RightNode = null;
node.Frequency = (int)(CharFrequencies[Key]);
node.Symbol = (string)(Key);
node.IsLeaf = true;
node.ParentNode = null;
Nodes.Add(node);
}
//Düğümlerin neye göre sıralanacağı NodeComparer sınıfındaki Compare metodunda tanımlıdır.
Nodes.Sort(new NodeComparer());
while(Nodes.Count > 1)
{
HuffmanNode node1 = (HuffmanNode)Nodes[0];
HuffmanNode node2 = (HuffmanNode)Nodes[1];
HuffmanNode newnode1 = new HuffmanNode();
newnode1.Frequency = node1.Frequency + node2.Frequency;
newnode1.IsLeaf = false;
newnode1.LeftNode = node1;
newnode1.RightNode = node2;
newnode1.Symbol = node1.Symbol + node2.Symbol;
node1.ParentNode = newnode1;
node2.ParentNode = newnode1;
Nodes.Add(newnode1);
Nodes.Remove(node1);
Nodes.Remove(node2);
Nodes.Sort(new NodeComparer());
}
}
Algoritmanın son adımı ise Huffman kodlarının oluşturulmasıdır. Programatik olarak kodlamanın en zor olduğu bölüm burasıdır. Zira burada huffman ağacı öz-yineli(recursive) olarak taranarak her bir düğümün huffman kodu atanacaktır. Performansı artırmak için semboller ve kod sözcükleri ayrıca bir Hashtable koleksiyonunda saklanmıştır. Böylece her bir kodun çözülmesi sırasında ağaç yapısı taranmayacak, bunun yerine Hashtable'dan ilgili kod bulunacaktır. Kodlamayı yapan metot aşağıdaki gibidir.
private void FindCodeWords(HuffmanNode Node)
{
HuffmanNode leftNode = Node.LeftNode;
HuffmanNode rightNode = Node.RightNode;
if(leftNode == null && rightNode == null)
Node.Code = "1"; if(Node == this.RootHuffmanNode)
{
if(leftNode != null)
leftNode.Code = "0";
if(rightNode != null)
rightNode.Code= "1";
}
else
{
if(leftNode != null)
leftNode.Code = leftNode.ParentNode.Code + "0";
if(rightNode != null)
rightNode.Code= rightNode.ParentNode.Code + "1";
}
if(leftNode != null)
{
if(!leftNode.IsLeaf)
FindCodeWords(leftNode);
else
{
CodeWords.Add(leftNode.Symbol[0].ToString(),leftNode.Code);
}
}
if(rightNode != null)
{
if(!rightNode.IsLeaf)
FindCodeWords(rightNode);
else
{
CodeWords.Add(rightNode.Symbol[0].ToString(),rightNode.Code);
}
}
}
Huffman algoritmasının temel basamakları bitmiş durumda. Bundan sonraki kodlar elde edilen sıkıştırılmış verinin ne şekilde dosyaya kaydedileceği ve sıkıştırılmış dosyanın nasıl tekrar geri elde edileceği ile ilgilidir. Bu noktada uygulamamız için bir dosya formatı belirlememiz gerekmektedir. Hatırlanacağı üzere sıkıştırılmış veriyi tekrar eski haline getirmek için frekans tablosuna ihtiyacımız vardır. Dolayısıyla sıkıştırılmış veriyi dosyaya yazmadan önce dosya formatımızın kurallarına göre sembol frekanslarını dosyaya yazmamız gerekir.
Benim programı yazarken geliştirdiğim dosya formatı aşağıdaki gibidir.
dosya.huff
-----------
1- ) İlk 4 byte --> Orjinal verideki toplam sembol sayısı.(ilk byte yüksek anlamlı byte olacak şekilde)
2 -) Sonraki 1 byte --> Data bölümünde bulunan son byte'taki ilk kaç bitin data'ya dahil olduğunu belirtir. (Data bölümündeki bitlerin sayısı 8’in katı olmayabilir.)
3 -) 2 byte Sembol + 4 byte sembol frekansı (bu bölüm ilk 4 byte'ta belirtilen sembol sayısı kadar tekrar edecektir.-ilk byte yüksek anlamlı byte olacak şekilde-)
4 -) Son bölümde ise sıkıştırılmış veri bit dizisi şeklinde yer alır.
Aşağıdaki metot yukarıda belirlenen kurallara göre sıkıştırılmış veriyi dosyaya .huff uzantılı olarak kaydedir.
[Not : Yazılacak programa göre bu dosya formatı değişebilir. Örneğin birden fazla dosyayı aynı anda sıkıştıran bir program için bu format tamamen değişecektir.]
public void WriteCompressedData()
{
/// 4 byte ->(uint) Sembol Sayısı(K adet)
/// 1 byte ->(uint) Data bölümünde bulunan son byte’taki ilk kaç bitin data’ya dahil olduğunu belirtir.
///
/// ------------------SEMBOL FREKANS BÖLÜMÜ------------------------------------------
///
/// 2 byte Sembol + 4 byte Sembol Frekansı
/// .
/// . K adet
/// .
/// 2 byte Sembol + 4 byte Sembol Frekansı
///
///
/// ------------------DATABÖLÜMÜ---------------------------------------
///
/// Bu bölümde Sıkıştırılmış veriler byte dizisi şeklinde yer alır.
///
/// Data bölümü (6*K + 6) numaralı byte’tan itibaren başlar.
///
int K = CharFrequencies.Keys.Count; /*K = 4 ise
*
* byte[0] = 0 0 0 0 0 1 0 0
* byte[1] = 0 0 0 0 0 0 0 0
* byte[2] = 0 0 0 0 0 0 0 0
* byte[3] = 0 0 0 0 0 0 0 0
*
* K(bits) = 00000100 00000000 00000000 00000000
* */
byte[] byteK = BitConverter.GetBytes(K);
FileStream fs = File.Open(this.NewFile,FileMode.Create,FileAccess.ReadWrite);
byte[] CompressedByteStream = GenerateCompressedByteStream();
WriteByteArrayToStream(byteK,fs);
fs.WriteByte(RemainderBits);
foreach(string sembol in CharFrequencies.Keys)
{
byte[] byteC = BitConverter.GetBytes((char)sembol[0]);
byte[] bytesFreqs = BitConverter.GetBytes((int)CharFrequencies[sembol]);
WriteByteArrayToStream(byteC,fs);
WriteByteArrayToStream(bytesFreqs,fs);
}
WriteByteArrayToStream(CompressedByteStream,fs);
fs.Flush();
fs.Close();
}
Kaynak







